ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ В ШРИФТАХ
ПОДГОТОВЛЕНЫ ДОЦЕНТОМ
Н. А. СОБОЛЕВЫМ

Пр иложение

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ В ШРИФТАХ

Работа по созданию шрифтов требует от графика знания ряда
■минимальных сведений по геометрическому черчению. Это необходи¬
мо как для правильного построения отдельных букв по их рисован¬
ным эскизам, так и для построения целых надписей и алфавитов
в единой геометрической системе.

Рассмотрим основные задачи из области геометрического чер¬
чения, наиболее часто встречающиеся при построении шрифтов.

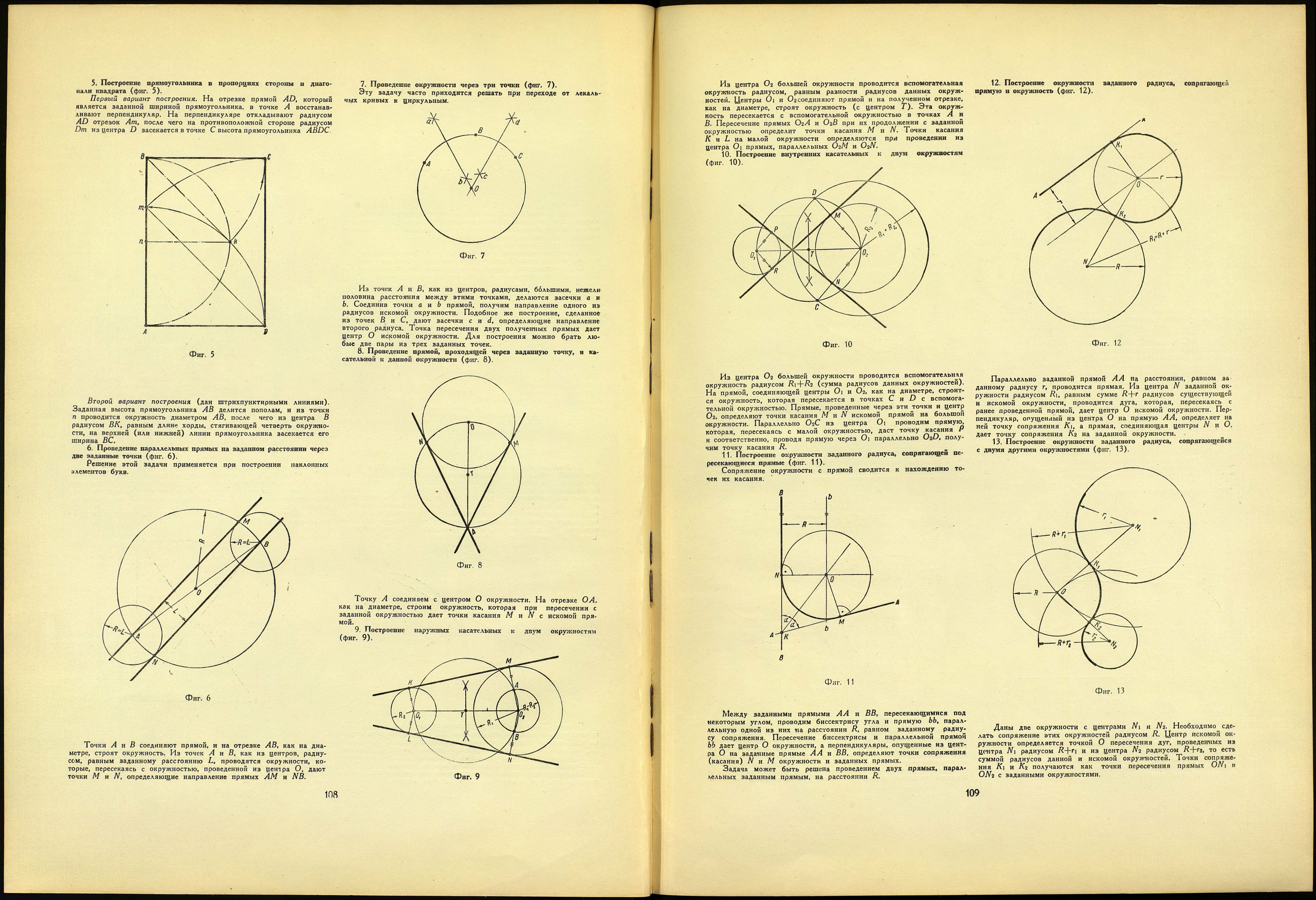
1. Деление отрезка прямой линии в данном отношении (фиг. 1).
Эта задача относится главным образом к членению литер по вер¬
тикали.

Ь

Фиг 1

Деление отрезка прямой AB на любое количество частей с лю¬
бым отношением их производится на основе свойств подобных тре¬
угольников. Из точки А данного отрезка прямой в произвольном
направлении проводим прямую. На этой вспомогательной прямом
в произвольном масштабе откладываем отрезки заданных отно¬
шений Ас, cd, db. Точка Ь на вспомогательной прямой
соединяется с точкой В. Через точки си d проводятся прямые, па¬
раллельные прямой ЬВ, которые в точках С и D пересечения их
отрезком AB делят его в данном отношении. В примере отрезок
прямой AB разделен на три части в отношении 1:2:3.

2. Деление отрезка прямой в золотом сечении (фиг. 2).

А

Фиг. 2

В точке В отрезка AB восстанавливается перпендикуляр. На
перпендикуляре откладывается отрезок ВС, равный половине отрез¬
ка AB. Точка А отрезка соединяется прямой с точкой С. На прямой
АС из точки С радиусом ВС делается засечка (то^ка D). Из точ¬
ки А радиусом AD делается засечка на прямой AB, дающая точку
Е. Отрезок AB в точке Е делится в золотом сечении.

Это построение можно не повторять в каждом случае, а поль¬
зоваться способом пропорционального деления отрезка.

3. Построение прямоугольника в пропорциях золотого сечения
(фиг. 3).

В,

Фиг. 3

Заданная высота прямоугольника AB делится пополам (точка
К), отрезок АК откладывается на перпендикуляре AD (точка т).
Точки Вит соединяются прямой, на которой радиусом тА из цен¬
тра т засекается точка п. Отрезок Вп переносится на верхнее осно¬
вание и определяет точку С. Прямоугольник ABCD будет построен
в пропорциях золотого сечения.

4. Построение прямоугольника в пропорциях египетского тре¬
угольника (фиг. 4).

Фиг. 4

Отрезок AB делится на четыре равные части. По ширине пря¬
моугольник должен иметь три такие единицы. Точки С и D могут
быть получены засечками из центров А и В радиусами, равными
трем и пяти единицам.

107